L’algorithme d’Huffman est un codage statistique, c’est-à-dire qu’il se base sur la fréquence d’apparition d’un fragment pour le coder : plus un fragment est fréquent, moins on utilisera de bits pour le coder. Prenons un exemple de fichier texte, si on considère que notre fragment est la taille d’un caractère, on peut remarquer que les voyelles sont beaucoup plus fréquentes que les consonnes : par exemple la lettre ‘e’ est largement plus fréquente que la lettre ‘x’, par conséquent la lettre ‘e’ sera peut-être codée sur 2 bits alors que la lettre ‘x’ en prendra 10.
Pour pouvoir compresser puis décompresser l’information, on va donc devoir utiliser une table de fréquences et deux choix s’offrent à nous : calculer une table et l’intégrer au fichier ou utiliser une table générique intégrée dans la fonction de compression.
- Dans le premier cas, la compression est meilleure puisqu’elle est adaptée au fichier à compresser, mais elle nécessite le calcul d’une table de fréquences et le fichier sera plus important également du fait de la présence de cette table dans le fichier.
- Dans le second cas, la compression sera plus rapide puisque elle n’aura pas à calculer les fréquences, par contre l’efficacité de la compression sera moindre et le gain obtenu par la première méthode (ratio de compression + taille de la table) peut être supérieur à celui de la deuxième (ratio de compression).
1) Création de la table d’apparition des fragments
Cette table consiste en un comptage des fragments au sein des données à compresser. Reprenons l’exemple d’un texte : nous allons analyser la phrase : "Ce TPE a pour objet la compression et le stockage". Pour simplifier l’exemple, nous ignorerons la casse (on ne prendra pas en compte les majuscules), ce qui donne la phrase : "ce tpe a pour objet la compression et le stockage".
| Lettres | Occurences | Fréquence |
|---|---|---|
| c | 3 | 6.12 % |
| e | 7 | 14.29 % |
| "espace" | 9 | 18.37 % |
| t | 3 | 6.12 % |
| p | 3 | 6.12 % |
| a | 3 | 6.12 % |
| o | 5 | 10.20 % |
| u | 1 | 2.04 % |
| r | 2 | 4.08 % |
| b | 1 | 2.04 % |
| j | 1 | 2.04 % |
| l | 2 | 4.08 % |
| m | 1 | 2.04 % |
| s | 3 | 6.12 % |
| i | 1 | 2.04 % |
| n | 1 | 2.04 % |
| k | 1 | 2.04 % |
| g | 1 | 2.04 % |
2) Création de l'arbre d'Huffman
L’arbre d’Huffman est la structure donnée qui va nous permettre de donner un code pour chaque lettre en fonction de sa fréquence.
Etape 1
Il faut commencer par trier la liste par ordre croissant de fréquences :
| Lettres | Occurences | Fréquence |
|---|---|---|
| b | 1 | 2.04 % |
| g | 1 | 2.04 % |
| i | 1 | 2.04 % |
| j | 1 | 2.04 % |
| k | 1 | 2.04 % |
| m | 1 | 2.04 % |
| n | 1 | 2.04 % |
| u | 1 | 2.04 % |
| l | 2 | 4.08 % |
| r | 2 | 4.08 % |
| a | 3 | 6.12 % |
| c | 3 | 6.12 % |
| p | 3 | 6.12 % |
| s | 3 | 6.12 % |
| t | 3 | 6.12 % |
| o | 5 | 10.20 % | e | 7 | 14.29 % |
| "espace" | 9 | 18.37 % |
Etape 2
Nous allons maintenant construire l’arbre à partir de la liste ordonnée de nœuds. La construction est très facile : il suffit de prendre les deux nœuds les moins fréquents (B et G) et de les ajouter comme fils d’un nouveau nœud qui aura pour fréquence la somme des deux :
Il suffit de réitérer cette étape jusqu'à ne plus avoir qu'un seul nœud. Après cela, descendre vers la gauche équivaut
à un 0, et descendre vers la droite à un 1.
On construit ainsi l'arbre suivant :
Pour coder un caractère, on part du tronc de l’arbre et on va vers les feuilles car lors de la décompression, partir des feuilles pourrait entraîner une confusion. Ainsi, la lettre b sera codée sur 6 bits : 111111, la lettre p sur 4 : 0111 et l’espace sur 2 : 00.
On en déduit le codage suivant :
| Lettres | Occurences | Nombre de bits | Codage |
|---|---|---|---|
| b | 1 | 6 | 111111 |
| g | 1 | 6 | 111110 |
| i | 1 | 6 | 111101 |
| j | 1 | 6 | 111100 |
| k | 1 | 6 | 111011 |
| m | 1 | 6 | 111010 |
| n | 1 | 6 | 111001 |
| u | 1 | 6 | 111000 |
| l | 2 | 5 | 11011 |
| r | 2 | 5 | 11010 |
| a | 3 | 5 | 11001 |
| c | 3 | 5 | 11000 |
| p | 3 | 4 | 0111 |
| s | 3 | 4 | 0110 |
| t | 3 | 3 | 101 |
| o | 5 | 3 | 100 | e | 7 | 3 | 010 |
| "espace" | 9 | 2 | 00 |
Avant compresion, la phrase occupait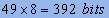 
.
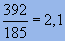Après compression, elle occupe 185 bits (sans l’en-tête). On a donc un quotient de compression de 
,
un taux de compression de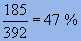 
et donc un gain de compression de 53 %.
En règle générale, un fichier texte est compressé par cette méthode suivant un gain de 30 à 60%.
Sur de très petits fichiers (moins de 1 Ko), l’en-tête est assez volumineux par rapport aux informations compressées.
Le fichier réduit a alors une taille supérieure au fichier original.
Sur de gros fichiers, on peut appliquer l’algorithme de Huffman non pas par caractère mais par tranche de 2, 3 ou 4 caractères.
Le problème est que la construction de l’arbre prend beaucoup plus de temps (l’arbre est plus gros, il y 65536 doublets
possibles de caractères ASCII étendu par exemple). De même, l’en-tête prend une place considérable.
4) Variantes de l'algorithme d'Huffman
Il existe 3 variantes de cet algorithme :
- Statique : Chaque octet possède un code prédéfini par le logiciel de compression. Ainsi, l’en-tête est déjà construit. Ce type de compression prend moins de temps et est assez efficace pour des fichiers correspondant au type pour lequel l’en-tête a été fabriqué, comme des fichiers texte dans une langue définie.
- Semi-adaptative : Le fichier est d’abord lu dans son intégralité et l’arbre est construit à partir de la fréquence de chaque octet. Ainsi, l’arbre sera propre au fichier compressé, mais il sera nécessaire de le transmettre dans l’entête pour permettre la décompression du fichier.
- Adaptative : L’arbre est construit au fur et à mesure de la lecture du fichier et il est sans cesse reconstruit. Cette méthode est plus lente que la méthode semi-adaptative mais offre de meilleurs résultats car l’arbre n’a pas besoin d’être stocké.